Confidence Interval and Bootstrapping <3-1>
<< 3주차 Lecture Note 1번째>>
- Sample and Population
- Central Limit Theorem
Sample and Population
앞선 강의에서 데이터로부터 moment를 구한 후 fit한 분포를 찾는 것을 배웠다.
이 때 구한 moment는 결국 분포의 파라미터와 연관되어 있는데,
문제는 '이 파라미터가 신뢰할만한가' 이다.
우리가 가진 데이터는 전체 데이터가 아닌 샘플 데이터이므로, 그로부터 구한 파라미터가 해당 분포에 정말 맞는 건지 의문이 생긴다.
이 때 의문을 해소하기 위한 방법이 '신뢰구간(confidence interval)'이다.
샘플 데이터로부터 동일한 파라미터를 반복해서 구하고, 그 수많은 파라미터가 어느 신뢰구간 안에 들어온 다면,
우리는 그 파라미터가 분포에 fit한 파라미터라고 볼 수 있다.
즉, 파라미터 검증을 위해 샘플로부터 파라미터를 반복 추정하는 거다.
Point Estimate on Single Sample
예제 데이터를 population으로 보고, 그로부터 딱 100개 의 row(샘플)만 가져와 샘플 파라미터를 구해보자.
어떤 경우에는 population과 분포가 유사할 것이고, 어떤 경우에는 전혀 맞지 않을거다.

Point Estimate on Multiple Sample
Single Sample로 분포 확인하는 과정을 여러번 반복해보자.
single sample 과 마찬가지로 오버피팅하는 케이스도 존재하고, 잘 맞는 케이스도 존재할거다.

왼쪽 그림은 100개의 sample에 대한 분포 그리는 과정을
300번 반복한 것이다(하늘색 라인).
푸른색 라인은 population 분포인데,
하늘색 라인에서 분명 과하게 튀는 케이스들이 많다는 걸 알 수 있다.
이제 100개의 sample에서 계산한 sample mean에 대한 분포를 보자.

sampling 을 반복하는 횟수가 많아질수록, 어떤 분포의 형태를 띄는 것을 볼 수 있다.
특히 N = 3000 일 때, 오른쪽으로 치우친 정규분포가 되는 것을 볼 수 있다.
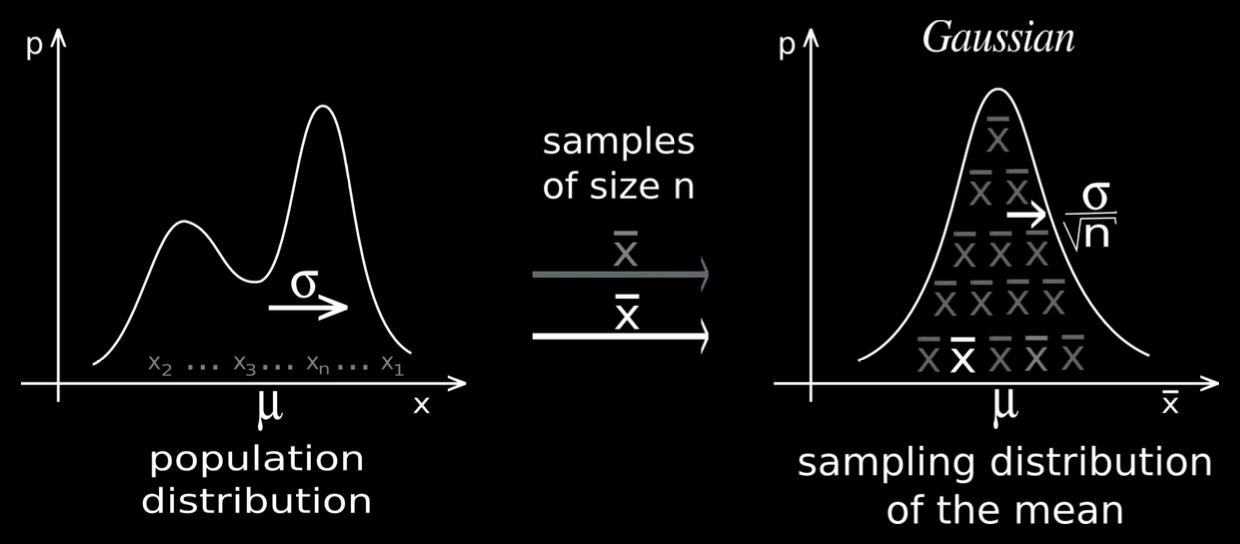
Central Limit Theorem
그렇다면 100개가 아닌 10,000개씩 sampling 해서 sample mean의 분포를 그려보면 어떨까?

N = 3000일 때, long tail을 갖지 않는 정규분포 형태가 나온다.
이 말인 즉, sample의 수가 커질수록 그 평균의 분포는 정규분포에 가까워진다는 것이다.
이를 중심극한정리(Central Limit Theorem) 이라고 한다.
중심극한정리란, sample \( n \)이 무한대로 갈 때, 그 샘플의 평균의 분포는 정규분포에 수렴하며,
sample mean은 population \( \mu \)에 수렴한다는 것이다.
또한, 이렇게 large n으로 구한 정규분포의 형태가 앞에서 언급한 신뢰구간으로 정의된다.
결론적으로,
우리가 데이터로부터 파라미터를 계산하고,
large n으로부터 sample parameter의 분포를 구해 신뢰구간을 추정함으로써
구한 파라미터가 신뢰구간 내부에 존재한다면, 분포 fit에 대한 검증이 가능하다는 것이다.
이로써 우리가 가진 데이터를 어느 분포에 fit할지 확실하게 판단이 가능해진다.